Question

Andtwo Brands is trying to decide if it should sell a new type of shirt. Fixed costs associated with the production of the shirts are estimated to be $850,000 with variable cost of $9 per unit. The shirts will sell for $15 each. The sales manager has been given a forecast that sales volume is likely to be anywhere between 100,000 and 300,000 shirts per year, so the expected value is 200,000. a) What is the break-even point? b) Is it reasonable to expect some profit from producing this product? c) Suppose the manager has decided that she will only produce the shirts if the company is likely to earn a profit of $250,000 or more. What do you think she will do?

Answer 1

The total cost for making N shirts will be given by the following equation:

`850000+9N`

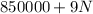
That is, the fixed cost plus the variable cost per unit multiplied by the total number of units produced.

The revenue will be the number of shirts sold (let's call it N too) multiplied by their price:

`15N`

The break-even point is the point at which the costs and revenues are equal. That will be the number of shirts that the company will have to produce and sell before beginning to obtain any profit. To find that number we just equate the two equations from above (costs and revenue) and solve for N:

`\begin{gathered} 15N=850000+9N \\ 15N-9N=850000 \\ 6N=850000 \\ N=(850000)/(6)=141667 \end{gathered}`

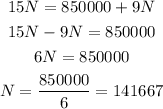
The company will have to sell at least 141667 shirts before having a

positive profit.

a) The break-even point is 141667 shirts.

b) Knowing that the company will have to sell 141667 shirts to make any profit, and they are expecting to sell 200000 in the year, they could expect profit the first year. However, considering that the forecast is between 100000 and 300000, there is still a probability of not selling enough shirts to make some profit.

Let's suppose they are able to sell 200000 shirts. The total profit that year will be:

`P=15N-(9N+850000)`

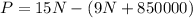
The first term is the revenue for selling, and the second in the parenthesis the total costs. Let's calculate the profit if 200000 shirts are sold:

`\begin{gathered} P=15\cdot200000-(9\cdot200000+850000) \\ P=3000000-2650000 \\ P=350000 \end{gathered}`

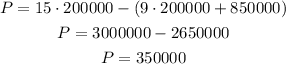
The profit would be $350000 the first year.

c) Now, if the manager decides the project is viable only if they earn a profit of $250000, we can calculate the number of shirts that they would have to sell to make that possible. recalling the equation for the profit:

`P=15N-(9N+850000)`

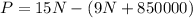
We want it to be $250000. Let's replace the value and solve for N:

`\begin{gathered} P=15N-(9N+850000)=250000 \\ 15N-9N-850000=250000 \\ 6N=250000+850000 \\ N=(1100000)/(6) \\ N=183333.33 \end{gathered}`

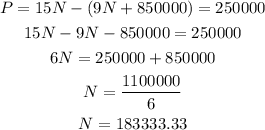
In order to earn a profit of at least $250000 the first year, the company will have to sell at least 183334 shirts. Therefore, if the forecast is accurate and they are able to sell 200000 shirts, the manager will approve the project. She will need to make sure at least 183334 shirts will be sold.