Question

Analyze the function f(x) = - 2 cot 3x. Include:

- Domain and range
- Period
- Two Vertical Asymptotes

Answer 1

The domain for the function is:
all real numbers except n π/3 where n is an an integer

The range for the function is:
all real numbers

The period is
π/3

Vertical asymptotes
x = n π/3 where n is an integer

Answer 2

Answer and Explanation :

Given : Function
`f(x)=-2\cot 3x`

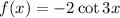
To find :

1) Domain and range

2) Period

3) Two Vertical Asymptotes

Solution :

1) Domain is defined as the set of possible values of x where function is defined.

`f(x)=-2\cot 3x`

`f(x)=-2((\cos 3x)/(\sin 3x))`

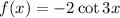
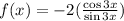
For domain,
`\sin3x\\eq 0`

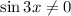
So,
`\sin3x\\eq \sin n\pi`

`3x\\eq n\pi`

`x\\eq (n\pi)/(3)`

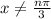
The value of x is define as
`x\\eq n\pi+(-1)^n(\pi)/(3)`

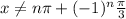
The domain of the function is all real numbers except
`x\\eq n\pi+(-1)^n(\pi)/(3)`

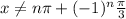
The range is defined as all the y values for every x.

So, The range of the function is all real numbers.

2) The general form of the cot function is
`y=A\cot (Bx-C)+D`

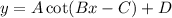
Where, Period is
`P=(\pi)/(|B|)`

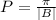
On comparing, B=3

So, The period of the given function is
`P=(\pi)/(|3|)`

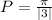
3) Vertical asymptote is defined as the line which approaches to infinity but never touches the line.

The vertical asymptote is at
`x= n\pi+(-1)^n(\pi)/(3)` where function is not defined.

The two vertical asymptote is

Put n=0,

`x= (0)\pi+(-1)^(0)(\pi)/(3)`

`x=(\pi)/(3)`

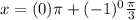
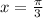
Put n=1,

`x= (1)\pi+(-1)^(1)(\pi)/(3)`

`x=\pi-(\pi)/(3)`

`x=(2\pi)/(3)`

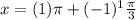
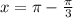
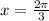
So, The two vertical asymptote are
`x=(\pi)/(3),(2\pi)/(3)`