Question

PLEASE help with these math questions

Answer 1

all of these are applications of the distance formula
remember a^2+b^2=c^2
so the distance (c) is
`\sqrt{a^(2)+b^(2)}`
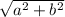
a and b are legnths of legs so we find the legnths


the distance between points (x1,y1) and (x2,y2) is

D=
`\sqrt{(x2-x1)^(2)+(y2-y1)^(2)}`
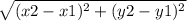
input points and find distance

1. (3,5) ot (7,3)
D=
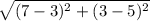
`\sqrt{(7-3)^(2)+(3-5)^(2)}`=√(16+4)=√20=4.47
answer is A

2. (-3,-2) to (4,6)
D=
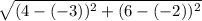
`\sqrt{(4-(-3))^(2)+(6-(-2))^(2)}`=√(49+64)=√113=10.63
answer is 10.6 units

3. from (1,7) to (9,-2)
D=
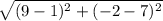
`\sqrt{(9-1)^(2)+(-2-7)^(2)}`=√(64+81)=√145=12.04
answer is B

4. (-1,-2) to (6,2)
D=
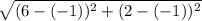
`\sqrt{(6-(-1))^(2)+(2-(-1))^(2)}`=√(49+16)=√65=8.06
round
8.1 units

5. apply multipule times
A=(2,2)
B=(12,2)
C=(9,8)
D=(2,8)
find the distance between
A to B
B to C
C to D
D to A
we can see the distances between AB, CD and AD easily
just since 1 variable doesn't change, we just find the change in the other variable
AB=10 units
CD=7 units
DA=6 units
now
CB is from (12,2) to (9,8)
D=
`\sqrt{(9-12)^(2)+(8-2)^(2)}`=√(9+36)=√45=6.7

add everybody
AB+BC+CD+DA=10+6.7+7+6=29.7
we see that they put a trick and see option D, the not careful people will chose that but the quesiton askes for the perimiter

answer is B