Question

The diameter of a circular park is 30m.Find its surface area.​

Answer 1

`\boxed{\boxed{\tt706.5 \: m {}^(2)}}`

Explanation:

Given:

`\rightarrow \sf \: Diameter = \tt \: 3 0 \: m`

To Find:

`\rightarrow\sf \: Surface\; Area`

Solution:

We know that the formula of Surface area of the circle is,

`\rightarrow \ttπ(r^2)`

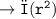
Where, R means Radius.

But we don't know what's the radius, So we'll use the formula where we can find the radius.

That is,

`\boxed{ \sf \: Formula \: of \: Radius = \cfrac{1}{2} * diameter}`

Now put the value of diameter:

`\sf{Radius} = \cfrac{1}{ 2} \: * \: 30 \: m`

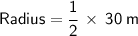
Solve it:

`\sf \: Radius = \cfrac{1}{ \cancel2 \: {}^(1) } * \cancel{30} \:^(15) m`

`\sf{Radius} = 1 * 15 \: m`

`\sf{Radius} =15 \: m`

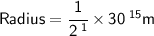
Now,

We know the value of Radius , So now let us use the formula of Surface area of a circle : (Then we can find the solution)

`\boxed{ \sf \: Surface \: area \: of \: the \: Circle =\pi(r {}^(2) )}`

We know that π = 3.14 .

So put the values accordingly:

`\sf \: Surface \: area \: of \: the \: Circle = 3.14( {15}^(2) )`

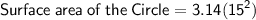
Solve it:

`\sf \: Surface \: area \: of \: the \: Circle =3.14(15 * 15)`

`\sf \: Surface \: area \: of \: the \: Circle =3.14(225) \: {}`

`\sf \: Surface \: area \: of \: the \: Circle =\boxed{\sf 706.5 \: {m}^(2)}`

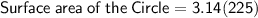
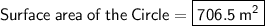
Hence, it's surface area would be 706.5 m^2.

`\rule{225pt}{2pt}`

I hope this helps!