ANSWER
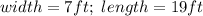
Step-by-step explanation
Let the length of the rectangle be L.
Let the width of the rectangle be W.
The length of the classroom is 2 feet shorter than three times its width. This implies that:
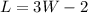
The area of a rectangle is given by:
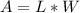
Hence, by substituting the given values into the equation, we have that:
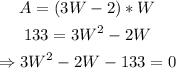
Solve the quadratic equation above by applying the quadratic formula:
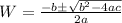
where
a = 3, b = -2, c = -133
Therefore:
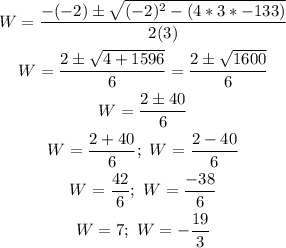
Since the width of a rectangle cannot be negative, the width of the rectangle is:
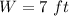
To find the length of the rectangle, substitute the value of W into the equation for L:
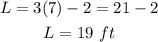
Hence, the width of the rectangle is 7 ft and its length is 19 ft.