Question

The table below shows the distance d(t) in meters that an object travels in t seconds:

t
(seconds)


d(t)
(meters)



1

15


2

60


3

135


4

240



What is the average rate of change of d(t) between 2 seconds and 4 seconds, and what does it represent?

50 m/s; it represents the average speed of the object between 2 seconds and 4 seconds

90 m/s; it represents the average speed of the object between 2 seconds and 4 seconds

90 m/s; it represents the average distance traveled by the object between 2 seconds and 4 seconds

50 m/s; it represents the average distance traveled by the object between 2 seconds and 6 seconds

Answer 1

Option B is correct

90 m/s; it represents the average speed of the object between 2 seconds and 4 seconds

Explanation:

Average rate of change(A(x)) for f(x) over interval [a,b] is given by:

`A(x) = (f(b)-f(a))/(b-a)`

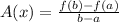
As per the statement:

here, d(t) is the distance in meter and t is the time in seconds.

For t = 2 seconds

then;

d(2) = 60 meters

and

for t =4 seconds

then;

d(4) = 240 meters

Then by definition of average rate we have;

`A(x) = (d(4)-d(2))/(4-2)`

⇒
`A(x) = (240-60)/(2)`

⇒
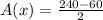
`A(x) = (180)/(2) = 90` m/s

Therefore, the the average rate of change of d(t) between 2 seconds and 4 seconds is, 90 m/s

It represents the average speed

Answer 2

The best answer to the physics question above would be the second statement. The average rate of change between 2 seconds and 4 seconds would be 50m/s and it represents the average speed of the object. The other choices do not point to the correct answer.