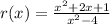So we need to find the polynomials p(x) and q(x) on each case. First of all its important to recognize a few important characteristics of each graph.
In graph a we can see a x-intercept in x=-1. The x-intercept is the point where the function r(x) is equal to 0. Since r(x) is equal to p(x)/q(x) then it's equal to 0 when p(x) is equal to 0. Then p(x) is a plinomyal that is equal to 0 when x=-1 so one possible expression for p(x) is:
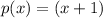
You can also note that there are two vertical asymptotes marked with dashed lines at x=-2 and x=-5. Vertical asymptotes occur at x values that make the denominator (i.e. q(x)) equal to 0. So we know that q(x) is equal to 0 when x=-2 and when x=-5. Then a possible expression for q(x) is:
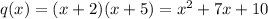
Finally, we should take a look at the horizontal asymptote. As you can see, as x increases the graph of the function approximates to the x-axis (i.e. to y=0). This also happens as x decreases so we can assume that for x tending to both positive and negative infinite the function r(x) tends to 0. This means that the horizontal asymptote is y=0. The only way this asymptote is 0 is that the degree of q(x) is greater than that of p(x). This is true for both the expressions since the degree of p(x) is equal to 1 whereas that of q(x) is equal to 2. Then the expressions chosen are correct and the function r(x) is given by:

And that's the answer to part a.
We are going to do something similar in part b. We have an x-intercept at x=-1 and vertical asymptotes at x=2 and x=-2. So p(x)=0 when x=-1 and q(x)=0 when x=2 and x=-2.
However, this time the horizontal asymptote is not y=0 but y=1. If the horizontal asymptote exists and is not 0 then both the numerator p(x) and the denominator q(x) must have the same degree and the asymptote is given by:
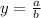
Where a and b are the leading coefficients of p(x) and q(x) respectively. Remember that the leading coefficients are the numbers multiplying the biggest power of x.
As I stated before there's a horizontal asymptote at y=1 so we can take a=1 and b=1.
So now we have all we need to build p(x) and q(x):
- p(x) must be 0 at x=-1, its leading coefficient must be 1 and its degree must be equal to that of q(x).
- q(x) must be 0 at x=2 and x=-2, its leading coefficient must be 1 and its degree must be equal to that of p(x).
We can propose this expression for q(x):
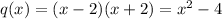
Its degree is two so for p(x) we can choose:
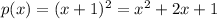
Then the answer to part b is: