Answer:
The domain of validity of the given identity is:
- All real numbers except nπ where n belongs to integers.
Explanation:
We are asked to prove the trignometric identity:
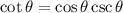
We know that:
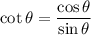
Hence, the function cotangent is defined where the denominator is not zero i.e. all the real numbers except where sine function is zero.
We know that the zeros of sine function are of the type: nπ where n belongs to integers.
Also, we can write the expression by:

We know that cosecant function is the reciprocal of the sine function.
i.e.
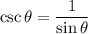
Hence, we get:
