Question

A window washer standing on a scaffold supported by a vertical rope at each end. The scaffold weighs 202 N and is 3.1 M long. What is the tension in each row but when the at 704 -N worker stands 1.06 M from one end?

Answer 1

Given,

The weight of the scaffold, W₁=202 N

The length of the scaffold, L=3.1 m

The weight of the worker, W₂=704 N

The distance from one of the ends of the scaffold, at which the worker is standing, d=1.06 m

In the diagram, T₁ and T₂ are the tensions in the rope.

Considering one of the ends of the scaffold as a pivot point, we can equate the total torque on the scaffold. Let us assume that the centre of mass of the scaffold is at the centre of the scaffold, i.e., at a distance of s=1.55 m

Let us consider point A to be the pivot point.

As the scaffold is balanced, the net torque on the scaffold is zero.

Thus,

`T_2* L=W_1* s+W_2* d`

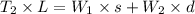
On substituting the known values,

`\begin{gathered} T_2*3.1=202*1.55+704*1.06 \\ \Rightarrow T_2=(202*1.55+704*1.06)/(3.1) \\ =338.46\text{ N} \end{gathered}`

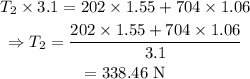
Thus the smaller tension is 338.46 N.

As the scaffold is in equilibrium, the net force on the scaffold is zero.

Equating all the vertical forces on the scaffold,

`T_1+T_2=W_1+W_2`

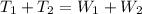
On substituting the known values,

`\begin{gathered} T_1+338.46=202+704 \\ \Rightarrow T_1=202+704-338.46 \\ =567.54\text{ N} \end{gathered}`

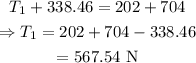
Thus the larger tension is 567.54