Question

Which pair of complex factors results in a real-number product?

a. 15(–15i)

b. 3i(1-3i)

c. (8 + 20i)(–8 – 20i)

d. (4+7i)(4-7i)

Answer 1

Answer: D

Explanation:

I did it and it is right :)

Answer 2

we will proceed to solve each case to determine the solution of the problem

we know that

`i^(2) =-1`

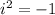
case A.
`15*(-15i)`

`15*(-15i)=-225i`

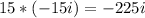
The result of case A is not a real number product

case B.
`3i*(1-3i)`

`3i*(1-3i)=3i*(1)-(3i)*(3i)\\=3i-9i^(2)\\=3i-9*(-1)\\=3i+9`

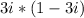
The result of case B is not a real number product

case C.
`(8+20i)*(-8-20i)`

`(8+20i)*(-8-20i)=8*(-8)+8*(-20i)+20i*(-8)-20i*(20i)\\=-64-160i-160i-400i^(2)\\=-64-320i-400*(-1)\\=-64-320i+400\\=336-320i`

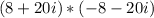
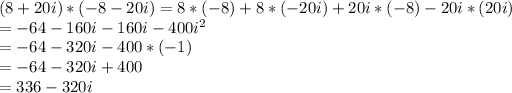
The result of case C is not a real number product

case D.
`(4+7i)*(4-7i)`

`(4+7i)*(4-7i)=4^(2) -(7i)^(2)\\=16-49i^(2)\\=16-49*(-1)\\=65\\`

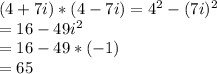
The result of case D is a real number product

therefore

the answer is the option

`(4+7i)*(4-7i)`