Question

What is the period and frequency of a 10-pound weight oscillating (as a pendulum) on a 5-meter-long rope?

Answer 1

Period = 4.5 seconds

Frequency = 0.22 hertz.

Explanation:

Given : 10-pound weight oscillating (as a pendulum) on a 5-meter-long rope.

To find : What is the period and frequency.

Solution :

The formula to find time when length is given,

`T=2\pi\sqrt{(L)/(g)}`

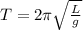
where,T is the time period , L is the length and g is the acceleration due to gravity

L= 5 m and g=9.8 m/s

Substitute in the formula,

`T=2\pi\sqrt{(5)/(9.8)}`

`T=2\pi√(0.510)`

`T=2* 3.14* 0.714`

`T=4.483`

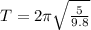
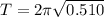
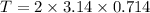
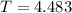
The time period is approx 4.5 seconds.

`\text{Frequency}=\frac{1}{\text{Period}}`

`\text{Frequency}=(1)/(4.5)`

`\text{Frequency}=0.22\text{hertz}`

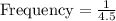
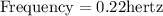
Therefore, Period = 4.5 seconds

Frequency is 0.22 hertz.

Answer 2

The mass of the pendulum does not affect the period and frequency
The period can be determined using the formula:
T = 2π √(L/g)

where L is the length of the rope
and g is the acceleration due to gravity = 9.8 m/s2

Plugging in the values:
T = 2π √(5/9.8)
T = 10π/7 = 4.49 s

And for the frequency:
f = 1/T
f = 1/4.49
f = 0.22 Hz