Question

A population of endangered birds decreases by 3% each year.

a. If the current population is 30,000 birds, write an equation that represents the number of birds, N, in terms of the number of years, T, from the present.

b. Approximately what will the bird population be after twenty years? Round your answer to the nearest thousand.

Answer 1

Answer: a) The required equation is,

`N=30000(0.97)^T`

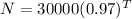
b) The approximately population of the birds after 20 years is 16314.

Explanation:

a) Since, the initial population, P = 30,000

The rate of increasing, r = 3% per year,

Hence, the population of birds after T years,

`N=P(1-(r)/(100))^T`

`\implies N = 30000(1-(3)/(100))^T`

`\implies N = 30000(1-0.03)^T`

`\implies N=30000(0.97)^T`

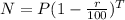
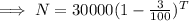
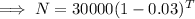
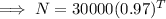
Which is the required equation.

b) Now, for T = 20 years,

The population of birds,

`N(20)=30000(0.97)^(20)=30000* 0.543794342927=16313.8302878\approx 16314`

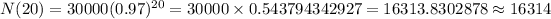
⇒ The approximately population of the birds after 20 years is 54183.

Answer 2

Since the number of bird decreases 3% per year then for year 1 there will be 29 100 birds left. This value is 97% of 30000. From this the number of birds for year 1 is N = 30000(1-0.03)

A. N = 30,000
`(1-0.03)^(2)`

B. To solve this we use the equation we established in letter A. We get the answer by substituting T with 20. N = 16,000.