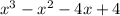Answer:
Option D is correct
The cubic polynomial function in standard form is :
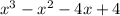
Explanation:
Given the zeroes of the polynomial function 1 , -2 and 2.
i.e, x = 1 , -2 and 2 where x is the zero of the polynomial function.
we can write this as
x - 1 = 0,
x + 2 = 0 or
x - 2 = 0
(x - 1)(x + 2)(x - 2) =0
Using identities
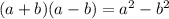
then;
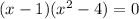
Multiply the first term of the first expression with second expression;
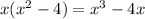
also,
Multiply the second term of the first expression with second expression;
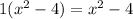
Now, subtract
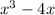 and
and
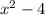
we get;

then, we have;
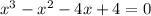
Cubic function is any function of the form
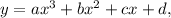 where a, b, c, and d are constants and a≠0
where a, b, c, and d are constants and a≠0
therefore, the given function is cubic function;
so, the cubic function f(x) =