Question

A student cycle 14km east from a and then 10km south east find the distance and bearing of b from a

Answer 1

Case: Cosine rule:

Given:

Method:

Using cosine rule:

`\begin{gathered} c^2=a^2+b^2-2bc\cos C \\ c^2=10^2+14^2-2(10)(14)\cos135\degree \\ c^2=100+196-280(-0.7071) \\ c^2=296+197.99 \\ c^2=493.99 \\ c=√(493.99) \\ c=22.226 \end{gathered}`

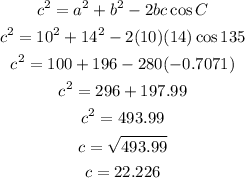
Next, we find the bearing of B from A.

This is the angle at A

Using sine Rule:

`\begin{gathered} (\sin A)/(a)=(\sin C)/(c) \\ (\sin A)/(10)=(\sin135)/(22.226) \\ \sin A=(10*\sin135)/(22.226) \\ \sin A=(10*0.7071)/(22.226) \\ \sin A=0.3181 \\ A=\sin^(-1)0.3181 \\ A=18.55\degree \end{gathered}`

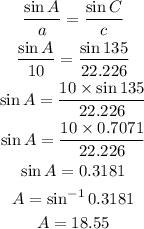
Final answer: To 3 and 2 decimal places

A) The distance between A and B is 22.226 hm

B) The bearing of B from A is 18.55 degrees