SOLUTION:
Case: Cosine rule:
Given:
Method:
Using cosine rule:
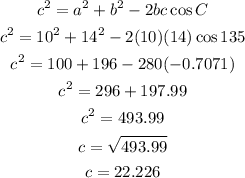
Next, we find the bearing of B from A.
This is the angle at A
Using sine Rule:
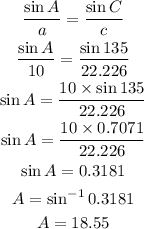
Final answer: To 3 and 2 decimal places
A) The distance between A and B is 22.226 hm
B) The bearing of B from A is 18.55 degrees