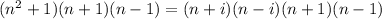Answer: Hello there!
here we have the equation n^4 - 1
using the relation:
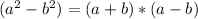
we can write our equation as:
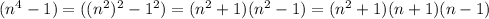
and (n^2 + 1) has only complex roots, i and - i, then we can factorize this as (n -i)(n + i) = n*n + ni - ni (+i)*(-i) = (n^2 + 1)
then our equation is: