Question

4. Women's heights have a mean of 63.6 in, and a standard deviation of 2.5 inches.a) Find the Z-score corresponding to a woman with a height of 70 inches and determinewhether the height is unusual.b) Find the Z-score corresponding to a woman with a height of 59 inches and determinewhether the height is unusual.c) Find the height of a woman whose height is 1.5 standard deviations below the mean.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about determine the Z-score.

First, remember the Z-score of a raw score x, given the population mean μ and the standard deviation σ can be calculated by the following formula:

`Z=(x-\mu)/(\sigma)`

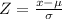
Also, remember that a Z-score is said to be unusual if it is more than 2 standard deviations away from the mean. Thinking of the distribution of the women's height as a graph:

Okay. So now we solve:

a) To find the Z-score corresponding to a women with a height of 70 inches.

Plugging x = 70, μ = 63.6 and σ = 2.5, we have:

`Z=(70-63.6)/(2.5)=(6.4)/(2.5)=0.375`

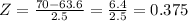
In this case, as the Z-score is something between -2 and 2, then it indicates we have an ordinary Z-score (means it is not unusual).

b) To find the Z-score corresponding to a woman with a height of 59 inches.

Plugging x = 59, μ = 63.6 and σ = 2.5, we get

`Z=(59-63.6)/(2.5)=(-4.6)/(2.5)=1.84`

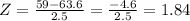
Again, since it is between -2 and 2, it is not unusual.

c) Find the height of a woman whose height is 1.5 standard deviation below the mean.

In this case, we know that Z = -1.5, such that we can plug μ = 63.6, σ = 2.5 and solve for x:

`-1.5=(x-63.6)/(2.5)`

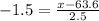
Multiply both sides of the equation by a factor 2.5

`-3.75=x-63.6`

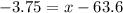
Add 63.6 on both sides of the equation

`x=59.2\text{ inches}`

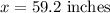
These are the answers for the questions.