Question

Cory writes the polynomial x^7+3x^5+3x+1. Melissa writes the polynomial x^7+5x+10. Is there a difference between the defree of the sum and the degree of the difference of the polynomials?

Answer 1

Answer: D- Adding their polynomials together results in a polynomial the degree 7, but subtracting one polynomial from the other results in a polynomial with degree 5.

Answer 2

Answer: Yes, the degree of sum is differ from the degree of difference.

Explanation:

Degree of a polynomial is a highest power of its monomials ( single term).

Here, the given polynomials are,

`x^7+3x^5+3x+1`

`x^7+5x+10`

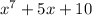
By adding these two polynomials,

`x^7+3x^5+3x+1+x^7+5x+10`

`=2x^7+3x^5+8x+11`

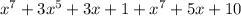
Since, the highest power of x in this result = 7

Hence, the degree of sum of the given polynomials = 7

Now, by subtracting the given polynomials,

`(x^7+3x^5+3x+1)-(x^7+5x+10`

`=x^7+3x^5+3x+1-x^7-5x-10`

`=3x^5-2x-9`

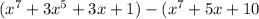
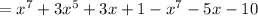
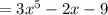
Since, the highest power of x in this result = 5,

Hence, the degree of difference of the given polynomials = 5

Thus, both the degree of sum and difference are different.