Question

Wyatt’s eye-level height is 120 ft above sea level, and Shawn’s eye-level height is 270 ft above sea level. How much farther can Shawn see to the horizon? Use the formula d = square root of 3h/2, h>0 with d being the distance they can see in miles and h being their eye-level height in feet.

Answer 1

Let

d-------> is the distance they can see in miles

h-------> is the eye-level height in feet

we know that

The formula to find the distance d is equal to

`d=\sqrt{(3h)/(2)}`

Step
`1`

Find the distance d for Wyatt’s eye-level

`h=120 ft`

`d=\sqrt{(3*120)/(2)}`

`d=√(180)`

`d=13.42`
`miles`

Step
`2`

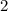
Find the distance d for Shawn’s eye-level

`h=270 ft`

`d=\sqrt{(3*270)/(2)}`

`d=√(405)`

`d=20.12`
`miles`

Step
`3`

Subtract the distance d for Shawn’s eye-level from the distance d for Wyatt’s eye-level

`=20.12-13.42\\`

`=6.70`
`miles`

therefore

the answer is

Shawn can see
`6.7`
`miles` farther

Answer 2

Using the formula given: d = √(3h/2)

We simply substitute the given values of h into the equation and compare the results.

For Wyatt where h = 120:
d = √(3(120)/2)
d = 13.42 miles

For Shawn where h = 270:
d = √(3(270)/2)
d = 20.12 miles

Since the question asks for how much farther can Shawn see, we subtract the results:

20.12 - 13.42 = 6.7

Therefore, Shawn can see 6.7 miles farther.