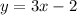Question

The ordered pairs (0, -2), (1, 1), (2, 4), (3, 7), and (4, 10) represent a function.  What is a rule that represents this function?

Answer 1

I just started doing function in my Algebra class. So what I was taught was there can't be more than 1 output aka "y" for one input aka "x".

So with the ordered pairs you have above is a function because there's only 1 output coming out. I have a picture showing why. It's labeled a purple one.
You know a graph or anything is not a function because it has more than 1 output which is not okay. For example: (1,6), (5,3), (2,9), and (1, 7) Now you notice that I have two coordinate pairs that have x for 1 and y for 6 and 7. I have another picture showing a example of a non-function.

Answer 2

`y=3x-2`

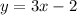
Explanation:

The given ordered pairs represents a linear function.

You can get this answer by observing the pattern between coordinates. You can observe, while x-values increases by one, y-values increases by 3. So, this can be expresses as a ratio of change

`m=(\Delta y)/( \Delta x)`

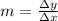
This ratio of change represents the slope of the linear function that models this set of ordered pairs. The ratio is

`m=(3)/(1)=3`

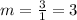
This means, the slope of the linear graph is 3.

Now, we use this slope and one point to find the exact relation that models this problem

`y-y_(1) =m(x-x_(1))\\y-(-2)=3(x-0)\\y+2=3x\\y=3x-2`

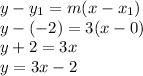
Therefore, the rule that represents this function is

`y=3x-2`