Given the data:
7.2, 8.7, 6.2, 8.2, 8.0, 6.8, 7.0, 9.2, 8.9, 5.8, 6.2, 8.2, 6.4, 6.1, 7.3
Let's find the 53rd percentile of the given data.
First rewrite the data values from the smallest to the greatest.
5.8, 6.1, 6.2, 6.2, 6.4, 6.8, 7.0, 7.2, 7.3, 8.0, 8.2, 8.2, 8.7, 8.9, 9.2
To find the 53rd percentile, apply the formula:
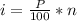
Where:
P = 53
n is the number of data values = 15
Thus, we have:
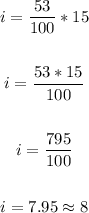
This means the 53rd percentile will be the 8th place data value when the data is arranged from the least to the greatest.
The 8th place data value is = 7.2
Therefore, the 53rd percentile is 7.2
ANSWER:
7.2