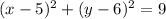Question

Find the equation of the circle whose center and radius are given.

center ( 5, 6), radius = 3

Answer 1

the general formula of the circle is (x-h)^2 + (y-k)^2 = r^2
where (h,k) the center of the circle and r is the radius
so , the equation is (x-5)^2 + (y-6)^2 = 9

Answer 2

`(x-5)^2+(y-6)^2 =9`

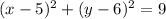
Explanation:

The equation of circle is given by:

`(x-h)^2+(y-k)^2 = r^2`

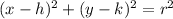
where,

(h, k) is the center

r is the radius of the circle.

As per the statement:

Given: center ( 5, 6), radius = 3 units

⇒(h, k) = (5, 6) and r = 3 units

Substitute these in [1] we have;

`(x-5)^2+(y-6)^2 = 3^2`

⇒
`(x-5)^2+(y-6)^2 =9`

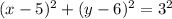
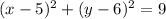
Therefore, the equation of the circle is,
`(x-5)^2+(y-6)^2 =9`