Question

ΔABC is reflected across line L to form Δ ALBLCL, and intersects line L at point D. Which equation is not necessarily true?

Answer 1

`A_LD= B_LD` is false statement.

B is correct

Explanation:

`\triangle ABC` is reflected across line L to form
`\triangle A_LB_LC_L`.

If we join A and
`A_L` and intersect line L at point D.

Reflection: A transformation of a geometric figure such that creating a mirror image across the line. The line of reflection is called axis of reflection.

As we know mirror image figure has same property their side measure and angle measure equal.

`\triangle ABC \text{ is congruent to }\triangle A_LB_LC_L`.

Distance of each vertex of figure from axis of reflection line is equal to their corresponding vertex.

Therefore, True statements are:-

`AD=A_LD`

`\angle ACB=\angle A_LC_LB_L`

`\angle BAC=\angle B_LA_LC_L`

`A_LD\\eq B_LD`

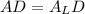
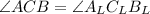
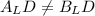
Please find the attached figure for reflection and coordinates.

Hence,
`A_LD= B_LD` is false statement.

Answer 2

option 2
ALD=BLD equation is not necessarily true, all other remaining equations satisfy laws of reflection.