Question

Suppose the orbit of a satellite around the earth can be approximated as a perfect circle. If the satellite is at an altitude of 1000 km above the earth’s surface, what is the orbital velocity of the satellite around the earth?

Answer 1

According to Kepler's Third Law, the period T of an object in a circular orbit with radius R around a mass M is given by the equation:

`T^2=(4\pi^2)/(GM)R^3`

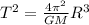
On the other hand, the tangential velocity of an object in circular motion in a trajectory with radius R and period T is:

`v=(2\pi R)/(T)`

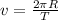
Use the first equation to find the period of the satellite around the Earth, using the radius of the Earth and the altitude of the satellite, as the following diagram shows:

The radius of the orbit of the satellite is the sum of the radius of the Earth and the altitude of the satellite.

Since the radius of the Earth is 6,371km and the altitude of the satellite is 1000km, then the radius R of the orbit of the satellite is:

`\begin{gathered} R=R_E+h \\ =6371km+1000km \\ =7371km \end{gathered}`

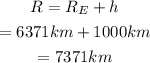
The mass of the Earth is 5.972*10^24kg, and the value of the gravitational constant G is:

`G=6.67*10^(-11)N\cdot(m^2)/(kg^2)`

Isolate T from Kepler's Third Law and substitute the values of R, M and G to find the period:

`\begin{gathered} T=\sqrt[]{(4\pi^2)/(GM)R^3} \\ =2\pi\cdot\sqrt[]{(R^3)/(GM)} \\ =2\pi\cdot\sqrt[]{((7371*10^3m)^3)/((6.67*10^(-11)N(m^2)/(kg^2))(5.972*10^(24)kg))} \\ =6300s \end{gathered}`

Replace R=7371km and T=6300s into the equation for the tangential velocity to find the orbital velocity of the satellite around the Earth:

`\begin{gathered} v=(2\pi R)/(T) \\ =(2\pi(7371km))/((6300s)) \\ =7.35(km)/(s) \end{gathered}`

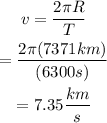
Therefore, the orbital velocity of the satellite around the Earth is 7.35 kilometers per second.