Question

A circle is defined by the equation x2 + y2 – x – 2y – 11/4 = 0. What are the coordinates for the center of the circle and the length of the radius?

Answer 1

x2 + y2 -x -2y -11/4 = 0
x2 -x +y2-2y-11/4 =0
we need to elliminate x , y from the equation and get the general form of the circle (x-k)^2 + (y-h)^2 = r^2 so,
[(x-1/2)^2 -1/4] + [(y-1)^2 -1] -11/4 = 0
(x-1/2)^2 + (y-1)^2 [ -1/4 -1-11/4] =0
(x-1/2)^2 + (y-1)^2 = 4
so the center of the circle is (1/2 , 1 )
and the rdius is √4 = 2

Answer 2

Coordinates of center is
`((1)/(2),1)` and length of the radius is 2 units

Explanation:

Given Equation of circle :
`x^2+y^2-x-2y-(11)/(4)=0`

We have to find coordinates of center and length of the radius.

consider,

`x^2+y^2-x-2y-(11)/(4)=0`

`x^2-x+y^2-2y-(11)/(4)=0`

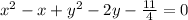
using completing the square method, we get

`x^2-x+(1)/(4)-(1)/(4)+y^2-2y+1-1-(11)/(4)=0`

`(x-(1)/(2))^2-(1)/(4)+(y-1)^2-1-(11)/(4)=0`

`(x-(1)/(2))^2+(y-1)^2-(1)/(4)-1-(11)/(4)=0`

`(x-(1)/(2))^2+(y-1)^2+(-1-4-11)/(4)=0`

`(x-(1)/(2))^2+(y-1)^2-(16)/(4)=0`

`(x-(1)/(2))^2+(y-1)^2=(16)/(4)`

`(x-(1)/(2))^2+(y-1)^2=2^2`

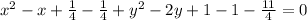
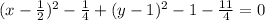
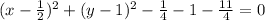
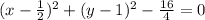
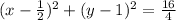
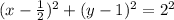
Now comparing with the standard form of the circle, (x-h)² + (y-k)² = r²

we get
`(h,k)=((1)/(2),1)` and r = 2

Therefore, Coordinates of center is
`((1)/(2),1)` and length of the radius is 2 units