Question

Alissa is analyzing an exponential growth function that has been reflected across the y-axis. She states that the domain of the reflected function will change because the input values will be the opposite sign from the reflected function. Simon disagrees with Alissa. He states that if an exponential function is reflected across the y-axis, the domain will still be all real numbers.

Answer 1

Simon is correct because even though the input values are opposite in the reflected function, any real number can be an input.

Answer 2

Consider the exponential function

`y=Ae^x`

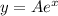
-----------(1)

and when it is reflected across y axis , it's equation becomes

`y=Ae^(-x)`

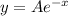
--------------------------(2)

As, domain of a function is defined as the set of all values of x , for which y is defined.

So, for function 1, domain is set of all real numbers.That is , x∈[-∞ ,∞]

And for function 2, which is reflection of function 1, it's domain will also be set of all real numbers.That is , x ∈ [-∞, ∞]

So, Simon is correct between Alissa and himself, as he is saying if an exponential function is reflected across the y-axis, the domain will still be all real numbers is true statement.