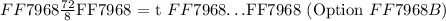Question

A jar at the fishing shop holds 72 worms. A cup holds 8 worms. How many times as many worms does the jar hold hold than the cup? Choose the equation that best represents the problem. 72-8=t72÷8=t72+8=t72×8=t

Answer 1

We are to determine the relationship between the capacity of a jar to cup that can hold the number of worms.

The following data is given to us in the question which expresses the number of worms that each type of container can hold:

`\begin{gathered} \text{Jar = 72 wroms} \\ \text{Cup = 8 }worms \end{gathered}`

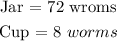
We are to determine the how many " times " more does the jar contains worms when compared to a cup.

Whenever we see the word " times " it always hints us towards finding the ratio. The ratio that will express the number of times more worms can be placed into a jar than in cup.

When writing ratio in the context of the above question we can say we need to find the ratio of number of worms ( jar ) : number of worms ( cup ).

The above ratio is due to the fact we know for sure that jar contains more worms as given in data as 72 worms and cup contains less worms, 8.

We will express the ratio in terms of fractions:

`(72)/(8)`

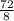
So the result of the fraction is:

`\begin{gathered} \frac{Worms\text{ in Jar}}{Worms\text{ in cup}}=(72)/(8)\text{ = 9} \\ \\ \text{Worms in Jar = }\text{\textcolor{#FF7968}{9}}\cdot Worms\text{ in cup} \end{gathered}`

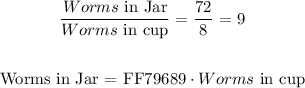
Therefore, the jar contains ( 9 ) times more worms than the cup. This answer most closely represents the form:

`\textcolor{#FF7968}{(72)/(8)}\text{\textcolor{#FF7968}{ = t }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ (Option }}\textcolor{#FF7968}{B)}`