Question

The sum of remainders obtained when x3+(k+8)x +k is divided by x-2 and when it is divided by x+1 is 0 fine the value of k

Answer 1

Answer: k=-5

Explanation:

The remainder theorem says that for any polynomial p(x) , if we divide it by the binomial x−a , the remainder is equal to the value of p(a) .

Therefore for
`p(x)=x^3+(k+8)x+k` if it is divided by x-2 and x+1 then its remainder must be p(2) and p(-1)

where,
`p(2)=2^3+(k+8)2+k=8+2k+16+k=3k+24`

`p(-1)=(-1)^3+(k+8)(-1)+k=-1-k-8+k=-9`

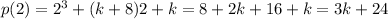
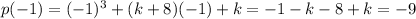
According to the question,

p(2)+p(-1)=0

`\Rightarrow3k+24-9=0\\\Rightarrow3k+15=0\\\Rightarrow3k=-15\\\Rightarrow\ k=(-15)/(3)\\\Rightarrow\ k=-5`