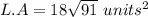GIVEN:
We are given a regular pyramid with the following dimensions;
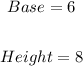
Required;
To calculate the lateral area.
Step-by-step solution;
To begin, we first take note that what we have is a regular pyramid with a hexagonal base. That is, the base has 6 sides.
Also, it is called a regular pyramid which means all sides of the base are equal.
We are given the formula for the lateral area as follows;

Where you have;

We now have;
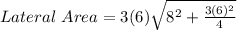
Now we can simplify;

We can however write the "exact answer" as follows;
ANSWER: