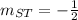Question

And the diagram PT St find the slope of st

Answer 1

You know that the lines PT and ST are perpendicular.

By definition, the slopes perpendicular lines are opposite reciprocal. This means that if the slope of a line is:

`m_1=a`

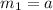
The slope of a perpendicular line to that line is:

`m_2=-(1)/(a)`

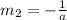
Knowing that:

`\begin{gathered} P\mleft(2,2\mright) \\ T\mleft(-1,-4\mright) \end{gathered}`

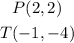
You can find the slope of the line PT using this formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where two points on the line are:

`\begin{gathered} (x_1,y_1) \\ (x_2,y_2) \end{gathered}`

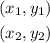
In this case, you can set up that for the line PT:

`\begin{gathered} y_2=-4_{} \\ y_1=2 \\ \\ x_2=-1 \\ x_1=2 \end{gathered}`

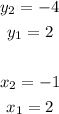
Then, substituting values into the formula and evaluating, you get:

`m_(PT)=(-4-2)/(-1-2)=(-6)/(-3)=2`

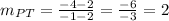
Knowing the slope of PT, you can determine that the slope of ST is:

`m_(ST)=-(1)/(2)`

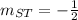
Hence, the answer is:

`m_(ST)=-(1)/(2)`