Question

FLP has vertices where F(-1,3), L(-3,1), P(-3,4). The figure was reflected about the x-axis. Describe the effect that took place after the transformation by identifying the coordinates of the new figure.

Answer 1

We have a figure FLP with certain coordinates, and we need to reflect these coordinates acroos the x-axis. To better understand this transformation, let's draw a coordinate plane with one point and reflect it across the x-axis, this is done below:

The red dot is the reflection of the black dot across the x-axis. The main concern we need to have is that the distance from the original point to the x-axis must be equal to the distance of the reflected point to the x-axis, but on the other side.

This means that whenever we perform this type of reflection the coordinates of the reflected point will be (x, -y). We only need to invert the signal of the "y" coordinate.

With this in mind we can solve the problem:

`\begin{gathered} F^(\prime)=(-1,-3) \\ L^(\prime)=(-3,-1) \\ P^(\prime)=(-3,-4) \end{gathered}`

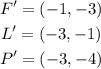
The green dots are the original points, and the red ones are the reflected points.