Question

A rectangular rug that has a length of 11 feet and a diagonal of 17 feet. Round your answer to the nearest tenth.

Answer 1

The area of a rectangle is given by the following equation:

`A\text{ =}b\cdot h`

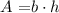
Where:

b = basis of the rectangle

h = height of the rectangle

Now, let's suppose that the basis is: b = 11

And from the statement we know that the diagonal is: d = 17

In order to find the area of the rectangle we need to find first the value of the height h. We can do that using Pitagoras theorem and the following picture:

Pitagoras theorem says that:

`d^2=b^2+h^2`

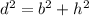
The sum of the square of the cathetus is equal to the square of the hyphotenuse.

From the last equation we find the value of the height h:

`\begin{gathered} h^2=d^2-b^2 \\ h=\sqrt[]{d^2-b^2}=\sqrt[]{17^2-11^2}=\sqrt[]{168}\cong12.96 \end{gathered}`

Using the last result we can compute the area of the rectangle:

`A=b\cdot h\cong11\cdot12.96\cong142.58\cong142.6`

So the final answer is: 142.6 ft²