Question

In a survey of women in the United States (ages 20-29) the mean height was 64.2 inches with a standard deviation of 2.9 inches.(a) What height represents the 95th percentile?(B) What height represents the first quartile

Answer 1

The height representing the 95th percentile is approximately 68.9705 inches, and the height for the first quartile (25th percentile) is approximately 62.2425 inches.

Step-by-step explanation:

In a survey of women in the United States (ages 20-29), the mean height was 64.2 inches with a standard deviation of 2.9 inches. To find the height that represents the 95th percentile, we can use the normal distribution properties. The 95th percentile in a normal distribution is often found by adding 1.645 (the z-score corresponding to the 95th percentile in a standard normal distribution) times the standard deviation to the mean. So, the height representing the 95th percentile would be 64.2 inches + (1.645 × 2.9 inches) = 64.2 + 4.7705 = 68.9705 inches.

For the first quartile, which is the 25th percentile, the z-score is approximately -0.675. The height representing the first quartile would be 64.2 inches - (0.675 × 2.9 inches) = 64.2 - 1.9575 = 62.2425 inches.

Answer 2

Given:

Mean = 64.2

Standard deviation = 2.9 inches

Let's solve for the following:

• (a). What height represents the 95th percentile?

At the 95th percentile, the z-score is 1.645

Apply the z-score formula:

`z=(x-\mu)/(\sigma)`

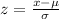
Where:

z = 1.645

μ = 64.2

σ = 2.9

Let's solve for x:

Rewrite the equation for x:

`\begin{gathered} x=z\sigma+\mu \\ \\ x=1.645*2.9+64.2 \\ \\ x=4.7705+64.2 \\ \\ x=68.97 \end{gathered}`

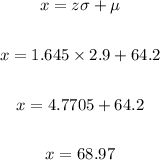
Therefore, the height that represents the 95th percentile is 68.97 inches.

• (b). , What height represents the first quartile?

We have:

The z-value for the height of the first quartile is:

P(Z < z) = 0.25

Using the standard normal distribution table, we have:

NORMSINV(0.25) = -0.67

z = -0.67

Now, apply the z-score formula:

`z=(x-\mu)/(\sigma)`

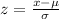
Where:

z = -0.67

u = 64.2

σ = 2.9

Let's solve for x:

`\begin{gathered} x=z\sigma+\mu \\ \\ x=-0.67*2.9+64.2 \\ \\ x=62.26 \end{gathered}`

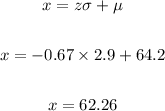
Therefore, the height that represents the first quartile is 62.26 inches.

ANSWER:

• (a). 68.97 inches

,

• (b). 62.26 inches