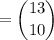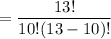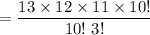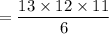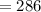Answer:
In 286 different ways 10 players can be selected.
Explanation:
There are 6 girls and 7 boys in a class. So in total there are 6+7 = 13 number of students in the class.
A team of 10 players is to be selected from the class.
As there is no other conditions are given, we can pick any 10 students from 13 students.
The way we can select 10 players from 13 students is,