Question

A boat is heading towards a lighthouse, where Jack is watching from avertical distance of 108 feet above the water. Jack measures an angle ofdepression to the boat at point A to be 9. (9 degrees). At some later time,Jack takes another measurement and finds the angle of depression to theboat (now at point B) to be 66. (66 degrees). Find the distance frompoint A to point B. Round your answer to the nearest tenth of a foot ifnecessary.

Answer 1

Given

A boat is heading towards a lighthouse, where Jack is watching from a

vertical distance of 108 feet above the water.

Jack measures an angle of depression to the boat at point A to be 9°.

At some later time, Jack takes another measurement and finds the angle of depression to the boat (now at point B) to be 66°.

To find: The distance from point A to point B.

Step-by-step explanation:

It is given that,

A boat is heading towards a lighthouse, where Jack is watching from a

vertical distance of 108 feet above the water.

Jack measures an angle of depression to the boat at point A to be 9°.

At some later time, Jack takes another measurement and finds the angle of depression to the boat (now at point B) to be 66°.

That imples,

Then,

`\begin{gathered} \tan9=(108)/(AC) \\ AC=(108)/(\tan9) \\ AC=681.89ft \end{gathered}`

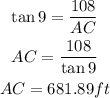
Also,

`\begin{gathered} \tan66=(108)/(BC) \\ BC=(108)/(\tan66) \\ BC=48.08ft \end{gathered}`

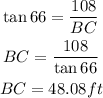
Therefore,

`\begin{gathered} AB=AC-BC \\ =681.89-48.08 \\ =633.81ft \\ =633.8ft \end{gathered}`

Hence, the distance from point A to point B is 633.8ft.