Given
A boat is heading towards a lighthouse, where Jack is watching from a
vertical distance of 108 feet above the water.
Jack measures an angle of depression to the boat at point A to be 9°.
At some later time, Jack takes another measurement and finds the angle of depression to the boat (now at point B) to be 66°.
To find: The distance from point A to point B.
Step-by-step explanation:
It is given that,
A boat is heading towards a lighthouse, where Jack is watching from a
vertical distance of 108 feet above the water.
Jack measures an angle of depression to the boat at point A to be 9°.
At some later time, Jack takes another measurement and finds the angle of depression to the boat (now at point B) to be 66°.
That imples,
Then,
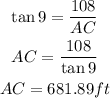
Also,
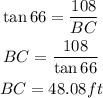
Therefore,
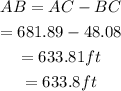
Hence, the distance from point A to point B is 633.8ft.