Question

, estimate the slope of the tangent line on the graph of

Answer 1

To estimate the sloep of the tangent line we first need to find an expression for the estimation, we know that this can be done by:

`m=(f(x+h)-f(x))/(h)`

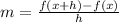
Then we have:

`\begin{gathered} m=(\lbrack6.8(x+h)^2-3.4(x+h)\rbrack-\lbrack6.8x^2-3.4x\rbrack)/(h) \\ =(\lbrack6.8(x^2+2xh+h^2)-3.4x-3.4h\rbrack-\lbrack6.8x^2-3.4x\rbrack)/(h) \\ =((6.8x^2+13.6xh+6.8h^2-3.4x-3.4h)-(6.8x^2-3.4x))/(h) \\ =(13.6xh+6.8h^2-3.4h)/(h) \\ =(h(13.6x+6.8h-3.4))/(h) \\ =13.6x+6.8h-3.4 \end{gathered}`

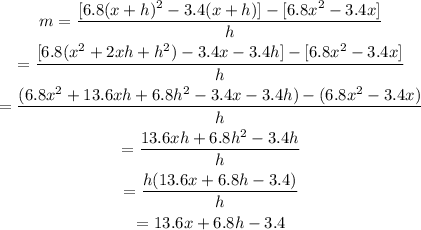
hence the estimation of the slope tangent line is:

`m=13.6x+6.8h-3.4`

To determine the slope at the given point for the value of h we just plug the values in the expression we found. for example for the first estimate we have:

`m=13.6(7)+6.8(1)-3.4=98.6`

doing this with all the other values of h we have:

h=1: m=98.6

h=0.5: m=95.2

h=0.1: m=92.48

h=0.01: m=91.868

h=0.001: m=91.8068