Question

Help! It says that I need to determine If both equations represent lines which are parallel, perpendicular, or none...

And then they give me two equations like
4x + 2y = 8
8x + 4y = -4y

Answer 1

4x + 2y = 8 (1)
8x + 4y = -4y (2)

A) Two lines are parallel if they have the same gradient
- putting both equations into the gradient- intercept form ( y = mx + c where m is the gradient)
(1) 4x + 2y = 8
2y = 8 - 4x
y = -2x + 4

(2) 8x + 4y = -4y
8x = -4y - 4y
y =
`(-8x)/(-8)`
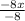
y = -x
Thus the gradient of the two equations are different and as such the two lines are not parallel

B) When two lines are perpendicular, the product of their gradient is -1

`m_(1) * m_(2) = p`
p = (-2) * (-1)
p = 2
∴ the two lines are not perpendicular either.

Thus these lines are SKEWED LINES