Question

A 1459 kg car is traveling WEST at 43 m/s. A 9755 kg truck is traveling EAST at 11 m/s. They collide head-on, and stick together.

Assuming EAST to be the positive direction, what is the velocity after this collision?

answer in m/s

Answer 1

Both vehicles move east at 3.97 m/s

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

It states that the total momentum of a system of bodies is conserved unless an external force is applied to it. The formula for the momentum of a body with mass m and speed v is:

P=mv.

If we have a system of two bodies, then the total momentum is the sum of both momentums:

`P=m_1v_1+m_2v_2`

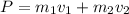
If a collision occurs and the velocities change to v', the final momentum is:

`P'=m_1v'_1+m_2v'_2`

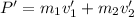
Since the total momentum is conserved, then:

P = P'

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2`

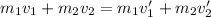
Assume both masses stick together after the collision at a common speed v', then:

`m_1v_1+m_2v_2=(m_1+m_2)v'`

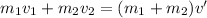
The common velocity after this situation is:

`\displaystyle v'=(m_1v_1+m_2v_2)/(m_1+m_2)`

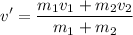
Assuming east direction to be positive, we have an m1=1459 kg car traveling west at v1=-43 m/s. An m2=9755 kg truck is traveling east at v2=11 m/s. They collide head-on and stick together after that.

Computing the resultant velocity after the collision:

`\displaystyle v'=(1459*(-43)+9755*11)/(1459+9755)`

`\displaystyle v'=(44568)/(11214)`

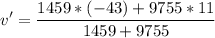
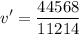
v' = 3.97 m/s

Both vehicles move east at 3.97 m/s