Question

Simplify square root of 5 multiplied by the cube root of 5.

5 to the power of 5 over 6
5 to the power of 1 over 6
5 to the power of 2 over 3
5 to the power of 7 over 6

Answer 1

5 to the power of 5 over 6 =
`5^{(5)/(6)}`

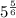
Explanation:

1)Let's define some properties about exponent:

`a^{(b)/(c)}=\sqrt[c]{a^(b)}`

For example :

`4^{(1)/(2)}=\sqrt[2]{4^(1)}=\sqrt[2]{4}=√(4)=2`

`2^{(6)/(3)}=\sqrt[3]{2^(6)}=\sqrt[3]{64}=4`

2)Another property of exponent is :

`(a^(b)).(a^(c))=a^(b+c)`

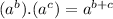
For example :

`(4^(2)).(4^(3))=4^(2+3)=4^(5)=1024`

This means that when we have two exponential functions with the same base that are multiplying between them, we can sum the exponents in order to make a new exponential function with the same base.

Using this two properties we can solve the problem.

• The expression is:

`(√(5)).(\sqrt[3]{5})`

• Using the two properties :

`(√(5)).(\sqrt[3]{5})=(5^{(1)/(2)}).(5^{(1)/(3)})=5^{(1)/(2)+(1)/(3)}`

Now,
`(1)/(2)+(1)/(3)=(5)/(6)`

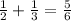
Therefore, the final expression is

`5^{(1)/(2)+(1)/(3)}=5^{(5)/(6)}` ⇒

`(√(5)).(\sqrt[3]{5})=5^{(5)/(6)}`

The correct answer is :

5 to the power of 5 over 6.