Question

What are the solutions to the quadratic equation (round to nearest hundredth) x2 + 6x
-6 = 0 ?

Answer 1

x = 0.88 OR x = -6.88

Explanation:

Given the quadratic equation:
`x^(2)` + 6x - 6 = 0

Applying the quadratic formula to determine the solutions, we have:

x = (-b ±
`\sqrt{b^(2) - 4ac}`) / 2a

where; a = 1, b = 6 and c = -6

x = ( -6 ±
`\sqrt{6^(2) -4 (1 * -6) }`) / 2

= ( -6 ±
`√(36 + 24)`) / 2

= (-6 ±
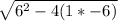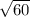`√(60)`) / 2

x = (-6 ± 7.75) / 2

So that,

x = (-6 + 7.75) / 2 OR x = (-6 - 7.75) / 2

x =
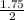`(1.75)/(2)` OR
`(-13.75)/(2)`

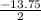
x = 0.88 OR -6.88

Thus, the solutions are: x = 0.88 OR x = -6.88