Question

Determine if the lines parallel, perpendicular, or neither. L1:3x - y = -9 L2: 32x +12y=-9

Answer 1

Neither

Step-by-step explanation:

Given the two lines below:

`\begin{gathered} L1\colon3x-y=-9 \\ L2\colon32x+12y=-9​ \end{gathered}`

First, express each line in the slope=intercept form (y=mx+b):

`\begin{gathered} L1\colon3x-y=-9\implies y=3x+9 \\ Slope\text{ of Line 1,}m=3 \end{gathered}`

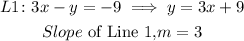
Similarly:

`\begin{gathered} L2\colon32x+12y=-9 \\ 12y=-32x-9 \\ y=-(32)/(12)x-(9)/(12) \\ y=-(8)/(3)x-(3)/(4) \\ \text{Slope of Line 2, }m=-(8)/(3) \end{gathered}`

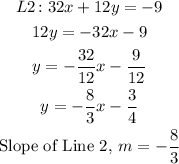
• For the lines to be parallel, the slopes must be equal.

,

• For the lines to be perpendicular, the product of the slopes must be -1.

Since none of these occurs, the lines are neither parallel nor perpendicular.