Question

In the diagram, point Ois the center of the circle and mzADB= 43°. If mcAO8= mzBOC, what is me.BDC?

Answer 1

An inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords. Using the following formula

`Inscribed\:Angle=(1)/(2)Intercepted\:Arc`

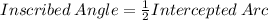
We have that

`m∠ADB=(1)/(2)mAB`

We have the measure of the angle ∠ADB, which is 43º. The arc AB is:

`mAB=2\cdot43=86`

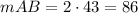
∠AOB is a central angle, therefore, the measure of the intercepted arc(which is AB) is equal to the measure of ∠AOB.

`mAB=m∠AOB=86^o`

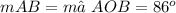
The measure of ∠AOB is equal to the measure of m∠BOC, therefore

`m∠BOC=86^o`

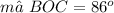
The angles ∠AOB and ∠BOC together create the central angle ∠AOC, that intercepts the arc AC, therefore

`86^o+86^o=mAC\implies mAC=172^o`

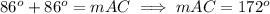
The arc AC is also intercepted by the chords that form the angle ∠ADC, therefore

`m∠ADC=(1)/(2)mAC\implies m∠ADC=86^o`

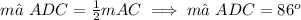
The angle ∠ADC is formed by the sum of the angles ∠ADB and ∠BDC, therefore, we have

`\begin{gathered} m∠ADC=m∠ADB+m∠BDC \\ \implies86^o=43^o+m∠BDC \\ \implies m∠BDC=43^o \end{gathered}`

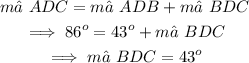
The measure of the angle ∠BDC is 43º.