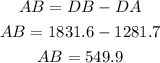Question

Mountain officials want to build a new ski lift from B to C, as shown in the figure below. The distance from A to C is 1480 feet. They measure angle DAC to be30° and angle DBC to be 22°. What is the distance from A to B ? Round your answer to the nearest tenth of a foot.

Answer 1

549.9 ft

Explanation:

We can calculate the value of AB, but first we must calculate the value of CD and DA by means of trigonometric ratios, finally I calculate the value of DB and from that value we subtract the value of DA and thus we will obtain the value of AB.

We calculate CD through sine and DA through cosine, just like this:

`\begin{gathered} \sin \theta=\frac{\text{ opposite}}{\text{hypotenuse}}\rightarrow\text{ opposite = }\sin \theta\cdot\text{ hypotenuse}\rightarrow\text{ opposite = }\sin 30\cdot1480 \\ CD=740 \\ \cos \theta=\frac{\text{ adjacent}}{\text{hypotenuse}}\rightarrow\text{ adjacent = }\cos \theta\cdot\text{ hypotenuse}\rightarrow\text{ adjacent = }\cos 30\cdot1480 \\ DA=1281.7 \end{gathered}`

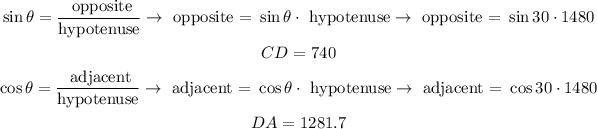
Now we calculate the value DB by means of that of the tangent of the angle of 22°, thus

`\begin{gathered} \tan \theta=\frac{\text{ opposite}}{\text{adjacent}}\rightarrow\text{ adjacent = }\frac{\text{ opposite}}{\tan \theta}\rightarrow\text{ adjacent = }(740)/(\tan 22) \\ DB=1831.6 \end{gathered}`

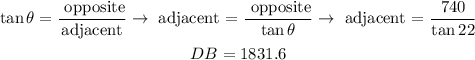
Now, AB would be:

`\begin{gathered} AB=DB-DA \\ AB=1831.6-1281.7 \\ AB=549.9 \end{gathered}`