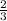Question

The quantity n varies jointly with the product of z and the square of the sum of x and y. When n is 18, x = 2, y = 1, and z = 3. What is the constant of variation?

Answer 1

Hello,

n=k*z*(x+y)²
with n=18,x=2,y=1 and z=3
==>18=k*3*(2+1)²
==>k=18/27=2/3

Answer 2

Constant of variation is,
`(2)/(3)`

Explanation:

Joint Variation states that it is jointly proportional to a set of variables i.e, it means that z is directly proportional to each variable taken one at a time.

Given the statement: The quantity n varies jointly with the product of z and the square of the sum of x and y.

"The square of sum of x and y" means
`(x+y)^2`

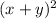
"Product of z and the square of the sum of x and z" means
`z * (x+y)^2`

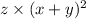
then; by definition we have;

`n \propto z * (x+y)^2`

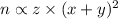
our equation will be of the form of:

`n = k \cdot z(x+y)^2` ......[1] ; where k is constant of Variation.

Given: n =18 , x =2 , y= 1 and z = 3

Solve for k;

Substitute these given values in [1] we have;

`18= k \cdot 3(2+1)^2`

Simplify:

`18= k \cdot 27`

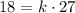
Divide both sides by 27 we get;

`k = (18)/(27) = (2)/(3)`

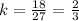
therefore, the constant of variation is,
`(2)/(3)`