Answer:
The expression for f(x) is:
f(x) = (x+5)(x+5)(x+5)(x+4)(x-2)(x-9)
Explanation:
We know that for any polynomial equation with roots:
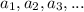 with multiplicity:
with multiplicity:
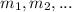
the equation for the polynomial is given by:

if the leading coefficient is negative we may take '-' sign in the starting of the expression.
Here we are given that :
f(x) has a leading coefficient of 1, roots –4, 2, and 9 with multiplicity 1, and root –5 with multiplicity 3
Hence, f(x) is given by:
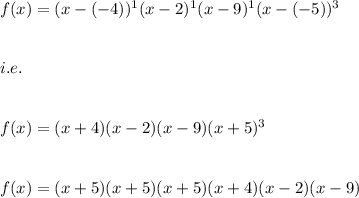
Hence, the expression for f(x) is:
