Question

Ja'Von kicks a soccer ball into the air. The function f(x) = –16(x – 2)2 + 64 represents the height of the ball, in feet, as a function of time, x, in seconds. What is the maximum height the ball reaches?

2feet

16 feet

32 feet

64 feet

Answer 1

D

Explanation:

Answer 2

Option D - 64 feet.

Explanation:

Given : Ja'Von kicks a soccer ball into the air. The function
`f(x) = -16(x-2)^2 + 64` represents the height of the ball, in feet, as a function of time, x, in seconds.

To find: What is the maximum height the ball reaches?

Solution :

To find the maximum height of the ball we find the derivative,

`f(x) = -16(x-2)^2 + 64`

Derivate w.r.t x

`f'(x) = -16* 2(x-2)+0`

`f'(x) = -32(x-2)`

To find maxima put
`f'(x)=0`

`0= -32(x-2)`

`32x=64`

`x=2`

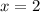
Now, we find the second derivative form maximum,

`f''(x) = -32<0`

Therefore, The maximum point is at x=2

Substitute x=2 in the given function,

`f(2) = -16(2-2)^2 + 64`

`f(2) = -16(0)+ 64`

`f(2) = 64`

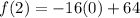
Therefore, Option D is correct.

The maximum height the ball reaches is 64 feet.