Question

Which statement best describes the excluded values of a rational expression?

a. The number of excluded values of a rational expression cannot exceed the degree of the numerator.
b. The number of excluded values of a rational expression cannot exceed the degree of the denominator.
c. The number of excluded values of a rational expression cannot exceed the sum of the degrees of the numerator and denominator.
d. The number of excluded values of a rational expression cannot exceed the difference in the degrees of the numerator and denominator.

Answer 1

Which statement best describes the excluded values of a rational expression?

B is the correct answer - The number of excluded values of a rational expression cannot exceed the degree of the denominator.

A rational expression is denoted in
`(p)/(q)` form; where 'p' is the numerator and 'q' is the denominator. The numerator and denominators can be polynomials. The denominator cannot be zero in general, as it makes the fraction value undefined.

Answer 2

Answer: b. The number of excluded values of a rational expression cannot exceed the degree of the denominator.

Explanation:

A rational expression is a fraction in which the numerator and the denominator are polynomials. The excluded values of a rational number are that values which make denominator zero.They are basically the zeroes of the polynomial of denominator.So,the number of excluded values can't exceed the degree of the denominator.

Here is a rational expression
`(x^2-6)/(x^2-4)`

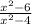
where the denominator is
`x^2-4=(x-2)(x+2)`

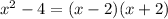
⇒x=-2,+2 are zero of polynomial
`x^2-4`

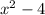
i.e. -2 and 2 are the excluded values for the whole rational expression.