Question

A rectangular garden is 6 feet long and 4 feet wide. A second rectangular garden has dimensions that are double the dimensions of the first garden. What is the percent of change in perimeter from the first garden to the second garden?

Answer 1

__________ _____________________
| 6 feet | | 6 feet | 6 feet |
| | | | | 4 feet
|_________ | |__________|__________|
| | |
| | | 4 feet
|__________|__________|

the figure shows that the second garden has a circumference twice . We must , however, prove.
Denote the sides of the first garden - a rectangle letters a and b
circuit garden
C₁ = 2a + 2b = 2*(a+b)
The sides of the second garden also denoted with the letters a and b . We calculate the circuit
C₂ = 2*2a + 2*2b = 4a + 4b = 4*(a+b)


`k = ( C_(2) )/( C_(1) ) = (4*(a+b))/(2*(a+b)) = (2*(a+b))/(1) = 2*(a+b)`

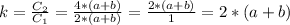
2 = 2*100%=200%
200% -100% = 100%

Answer : The ratio of the second garden to the first ( ratio ) is 2 . Circuit increased by 100 %

Answer 2

double dimentions
perimiter

P=2(L+W)

if we have
L=6
W=4
P=2(6+4)
P=2(10)
P=20
original is 20
if both are doubled

6*2=12
4*2=8
P=2(12+8)
P=2(20)
P=40


from original to new is
from 20 to 40
what is percent change?
find chnage
new-original=change
40-20=20
percent change=change/original
20/20=1=100%

answer is 100%