Question

I already solved for B but i need help with line a and c

Answer 1

Step 1. We know the measure of all of the angles in the triangle and the measure of side b:

Required: Find the measure of sides a and c to the nearest tenth.

Step 2. To find a and c we use the law of sines.

A, B, and C are the angles of the triangle and a, b, and c are the sides. The law of sines is:

`(a)/(sinA)=(b)/(sinB)=(c)/(sinC)`

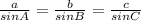
In our case, substituting the known values:

`(a)/(sin60)=(53)/(sin42)=(c)/(sin78)`

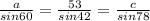
Step 3. Using the first equality we can find the value of a:

`(a)/(s\imaginaryI n60)=(53)/(s\imaginaryI n42)`

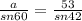
Solving for a:

`a=(53)/(s\imaginaryI n42)* sin60`

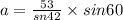
Solving the operations:

`\begin{gathered} a=(53)/((0.669130606))(0.866025403) \\ \downarrow \\ \boxed{a=68.6} \end{gathered}`

The result is already rounded to the nearest tenth.

Step 4. Using the second equality from step 2

`(53)/(sin42)=(c)/(sin78)`

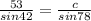
We will be able to find the value of c.

Solving for c:

`sin78*(53)/(sin42)=c`

Solving the operations:

`\begin{gathered} (0.9781476)(53)/((0.669130606))=c \\ \downarrow \\ \boxed{77.5=c} \end{gathered}`

The result is already rounded to the nearest tenth.

Answer:

`\begin{gathered} \boxed{a=68.6} \\ \boxed{c=77.5} \end{gathered}`